JavaFX combinado con Java permite una mejora substancial a nivel visual y de rendimiento de nuestras aplicaciones.
También hace una marcada separación entre el diseño visual y el desarroyo de la aplicación como veremos más adelante.
Por otra parte Scene Builder permite crear la interfaz gráfica de Java de forma más simple y cómoda.
> Instalación en base al siguiente software:
Windows 10
Apache NetBeans IDE 11.3
> Lo que vamos a instalar:
JavaFX Windows SDK 13.0.2
JavaFX Scene Builder 11.0.0
1- Descargar e instalar:
> Java FX:
https://gluonhq.com/products/javafx/
Una vez descargado, descomprimir el fichero "openjfx-13.0.2_windows-x64_bin-sdk.zip" en la raiz de la unidad C:
"C:\java fx-sdk-13.0.2\"
> Scene Builder:
https://openjfx.io/
Una vez descargado se instala todo por defecto.
2- Integrar "Javafx-sdk" en Netbeans:
Iniciamos NetBeans -> Tools -> Libraries -> [New Library]
Library Name: JavaFX
Library Type: Class Libreries
[OK]
Seleccionamos en la columna lateral izquierda la librería que acabamos de crear: JavaFX
Nos vamos a la pestaña "ClassPath" y pulsamos [Add Jar/Folder...]
Buscamos la carpeta donde tenemos puesto Javafx-sdk. En este caso fue guardado en:
C:\javafx-sdk-13.0.2\
Dentro la carpeta .\lib\, seleccionamos todos los ficheros con extensión ".jar" y pulsamos [Add Jar/Folder].
Finalmente salimos pulsando [Ok]
2.1- Añadir librerías al proyecto:
Creamos nuevo proyecto:
File -> New Proyect -> Java with Ant -> Java Aplication -> [Next]
Project name: PrimerJavaFX -> [Finish]
Le añadimos las librerías (click derecho sobre el proyecto):
Properties -> Libraries -> Compile -> Class-path -> [+] -> Add Library -> JavaFX [Add Library]
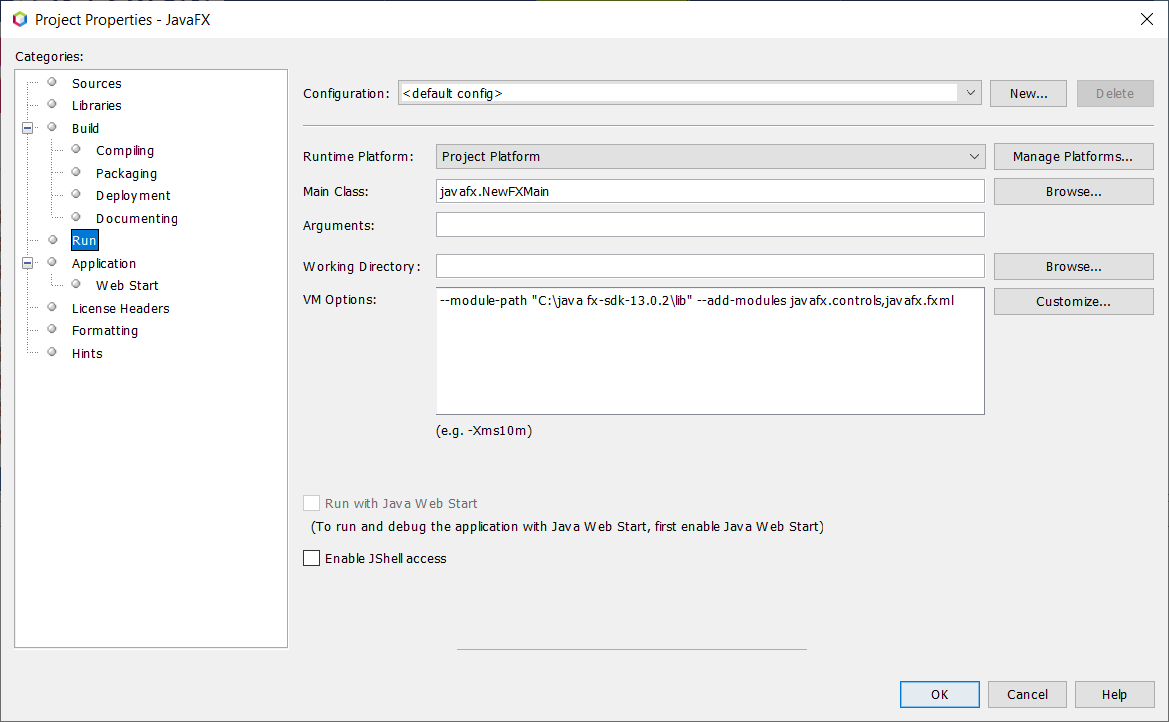
Y añadimos un código en la VM (click derecho sobre el proyecto):
Properties -> Libraries -> Run ->
VM Options:
--module-path "C:\java fx-sdk-13.0.2\lib" --add-modules javafx.controls,javafx.fxml
3- Integrar "Scene Builder" en Netbeans:
Iniciamos NetBeans -> Tools -> Options -> Java -> JavaFX ->
Scene Builder Home: C:\Program Files\SceneBuilder
Principio de mediocridad viene a decir que "cualquier cosa seleccionada al azar que observemos en un momento determinado no estará ni al comienzo ni al final de su vida, lo más probable es que esté en algún punto alrededor de la mitad de su vida". Partiendo de esta premisa sería posible calcular matemáticamente el tiempo que puede durar algo, y ese algo que vamos a intentar calcular va a ser el tiempo de vida que le queda a la epidemia del Coronavirus (o COVID-19).
Podría considerarse algo profético o mágico pero la "Inecuación de Gott" intenta calcular ese tiempo partiendo de un solo dato: el tiempo transcurrido desde el inicio del evento.
Fórmula:
ta * |(f - 1)/(f + 1)| < tr < ta * |(f + 1)/(f - 1)|
ta = tiempo transcurrido
tr = tiempo restante
f = fiabilidad que le queremos dar al resultado (%)
Datos recopilados para el cálculo:
1- Primer infectado: 12 de diciembre de 2019
2- Fecha actual: 29 de febrero de 2020
3- Tiempo transcurrido desde la fecha del primer infectado hasta fecha de hoy:
19 días (diciembre) + 31 días (enero) + 29 días (febrero) = 117 días
4- Se decide aplicar una fiabilidad del 50%
Resultado aplicando la fórmula:
Fin de la epidemia con una fiabilidad del 50%:
-> entre 9 de abril del 2020 y el 14 de febrero del 2021
Ahora solo hace falta esperar si el resultado se va ajustar a la realidad, el tiempo dirá...
Empecemos el proyecto desde Netbeans:
Crearemos un JFrame (ventana) al que añadiremos:
· 4 jTextField con sus respectivas labels
· 1 jSlider
· 2 jButton
Código java:
import java.text.DecimalFormat;
public class Main extends javax.swing.JFrame {
// Definicion variables
double ta1, tr0, tr1, f;
DecimalFormat df = new DecimalFormat("#.00");
// Cálculo medidas rectangulo áureo
final double Aureo = ((1 + Math.sqrt(5)) / 2);
int a = 512;
int b = (int) (a / Aureo);
final int width = a + b;
final int height = a;
public Main() {
initComponents();
this.setBounds(0, 0, width, height);
this.jPanel1.setBounds(0, 0, width, height);
this.setLocationRelativeTo(null);
}
private void initComponents() { ... aqui va el código generado automáticamente por NetBeans al crear la GUI ... }
private void jButtonCalcularActionPerformed(java.awt.event.ActionEvent evt) {
calcular();
}
private void jSlider1StateChanged(javax.swing.event.ChangeEvent evt) {
jTextField_Fiabilidad.setText("" + jSlider1.getValue());
calcular();
}
private void jButtonLimpiarActionPerformed(java.awt.event.ActionEvent evt) {
jTextField_TA1.setText("1");
jSlider1.setValue(50);
jTextField_Fiabilidad.setText("50");
// Intervalo
jTextField_TR0.setText(df.format(0d));
jTextField_TR1.setText(df.format(0d));
}
private void calcular() {
ta1 = Double.parseDouble(jTextField_TA1.getText());
f = Double.parseDouble(jTextField_Fiabilidad.getText()) / 100d;
// Inecuación de Gott
tr0 = ta1 * (Math.abs((f - 1) / (f + 1)));
tr1 = ta1 * (Math.abs((f + 1) / (f - 1)));
// Mostrar
jTextField_TR0.setText(df.format(tr0));
jTextField_TR1.setText(df.format(tr1));
}
public static void main(String args[]) {
java.awt.EventQueue.invokeLater(() -> {
new Main().setVisible(true);
});
}
}
Resultado:
Se muestra diagrama conceptual para entrenamiento de una red neuronal multicapa.
El proceso por pasos:
01- Obtener un Dataset en bruto(raw).
02- Discretizar Dataset [Dataset -> Dataset'].
03- Extraer Entradas(E) y Salidas(D) del Dataset'.
04- Pasar Entradas(E) por la Red Neuronal(RN).
05- Obtener Salidas(Y) de la RN.
06- Calcular Error(δ) en base a las Salidas(Y) de la RN y Salida(D) del Dataset'.
07- En base al cálculo del Error(δ), ajustar pesos(W) de la RN.
08- Pasar al siguiente registro del Dataset' volviendo de nuevo al punto 03. Si no existen más registros se pasa al punto 09.
09- Finalizados los registros del Dataset' volver a posicionarse en el 1º registro y volver a empezar desde punto 03, siempre y cuando el Error(δ) general sea inferior o igual (<=) alumbral especificado por el usuario. En tal caso da por finalizado el entrenaminento.