JavaFX combinado con Java permite una mejora substancial a nivel visual y de rendimiento de nuestras aplicaciones.
También hace una marcada separación entre el diseño visual y el desarroyo de la aplicación como veremos más adelante.
Por otra parte Scene Builder permite crear la interfaz gráfica de Java de forma más simple y cómoda.
> Instalación en base al siguiente software:
Windows 10
Apache NetBeans IDE 11.3
> Lo que vamos a instalar:
JavaFX Windows SDK 13.0.2
JavaFX Scene Builder 11.0.0
1- Descargar e instalar:
> Java FX:
https://gluonhq.com/products/javafx/
Una vez descargado, descomprimir el fichero "openjfx-13.0.2_windows-x64_bin-sdk.zip" en la raiz de la unidad C:
"C:\java fx-sdk-13.0.2\"
> Scene Builder:
https://openjfx.io/
Una vez descargado se instala todo por defecto.
2- Integrar "Javafx-sdk" en Netbeans:
Iniciamos NetBeans -> Tools -> Libraries -> [New Library]
Library Name: JavaFX
Library Type: Class Libreries
[OK]
Seleccionamos en la columna lateral izquierda la librería que acabamos de crear: JavaFX
Nos vamos a la pestaña "ClassPath" y pulsamos [Add Jar/Folder...]
Buscamos la carpeta donde tenemos puesto Javafx-sdk. En este caso fue guardado en:
C:\javafx-sdk-13.0.2\
Dentro la carpeta .\lib\, seleccionamos todos los ficheros con extensión ".jar" y pulsamos [Add Jar/Folder].
Finalmente salimos pulsando [Ok]
2.1- Añadir librerías al proyecto:
Creamos nuevo proyecto:
File -> New Proyect -> Java with Ant -> Java Aplication -> [Next]
Project name: PrimerJavaFX -> [Finish]
Le añadimos las librerías (click derecho sobre el proyecto):
Properties -> Libraries -> Compile -> Class-path -> [+] -> Add Library -> JavaFX [Add Library]
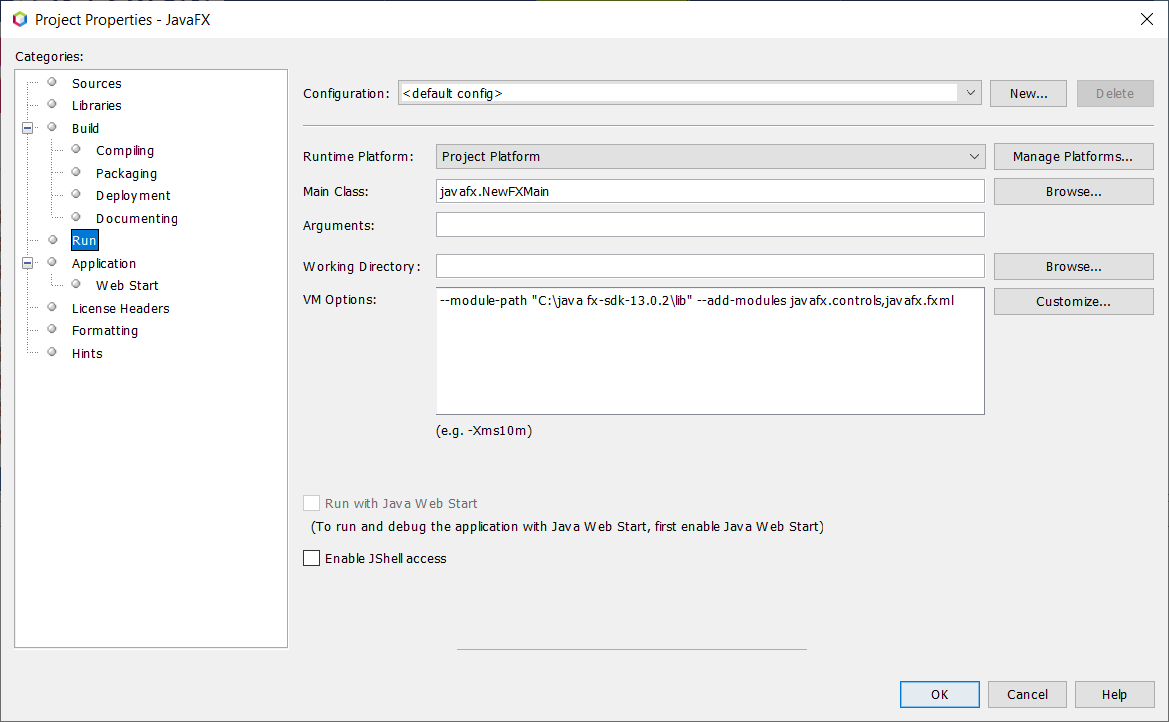
Y añadimos un código en la VM (click derecho sobre el proyecto):
Properties -> Libraries -> Run ->
VM Options:
--module-path "C:\java fx-sdk-13.0.2\lib" --add-modules javafx.controls,javafx.fxml
3- Integrar "Scene Builder" en Netbeans:
Iniciamos NetBeans -> Tools -> Options -> Java -> JavaFX ->
Scene Builder Home: C:\Program Files\SceneBuilder
Principio de mediocridad viene a decir que "cualquier cosa seleccionada al azar que observemos en un momento determinado no estará ni al comienzo ni al final de su vida, lo más probable es que esté en algún punto alrededor de la mitad de su vida". Partiendo de esta premisa sería posible calcular matemáticamente el tiempo que puede durar algo, y ese algo que vamos a intentar calcular va a ser el tiempo de vida que le queda a la epidemia del Coronavirus (o COVID-19).
Podría considerarse algo profético o mágico pero la "Inecuación de Gott" intenta calcular ese tiempo partiendo de un solo dato: el tiempo transcurrido desde el inicio del evento.
Fórmula:
ta * |(f - 1)/(f + 1)| < tr < ta * |(f + 1)/(f - 1)|
ta = tiempo transcurrido
tr = tiempo restante
f = fiabilidad que le queremos dar al resultado (%)
Datos recopilados para el cálculo:
1- Primer infectado: 12 de diciembre de 2019
2- Fecha actual: 29 de febrero de 2020
3- Tiempo transcurrido desde la fecha del primer infectado hasta fecha de hoy:
19 días (diciembre) + 31 días (enero) + 29 días (febrero) = 117 días
4- Se decide aplicar una fiabilidad del 50%
Resultado aplicando la fórmula:
Fin de la epidemia con una fiabilidad del 50%:
-> entre 9 de abril del 2020 y el 14 de febrero del 2021
Ahora solo hace falta esperar si el resultado se va ajustar a la realidad, el tiempo dirá...
Empecemos el proyecto desde Netbeans:
Crearemos un JFrame (ventana) al que añadiremos:
· 4 jTextField con sus respectivas labels
· 1 jSlider
· 2 jButton
Código java:
import java.text.DecimalFormat;
public class Main extends javax.swing.JFrame {
// Definicion variables
double ta1, tr0, tr1, f;
DecimalFormat df = new DecimalFormat("#.00");
// Cálculo medidas rectangulo áureo
final double Aureo = ((1 + Math.sqrt(5)) / 2);
int a = 512;
int b = (int) (a / Aureo);
final int width = a + b;
final int height = a;
public Main() {
initComponents();
this.setBounds(0, 0, width, height);
this.jPanel1.setBounds(0, 0, width, height);
this.setLocationRelativeTo(null);
}
private void initComponents() { ... aqui va el código generado automáticamente por NetBeans al crear la GUI ... }
private void jButtonCalcularActionPerformed(java.awt.event.ActionEvent evt) {
calcular();
}
private void jSlider1StateChanged(javax.swing.event.ChangeEvent evt) {
jTextField_Fiabilidad.setText("" + jSlider1.getValue());
calcular();
}
private void jButtonLimpiarActionPerformed(java.awt.event.ActionEvent evt) {
jTextField_TA1.setText("1");
jSlider1.setValue(50);
jTextField_Fiabilidad.setText("50");
// Intervalo
jTextField_TR0.setText(df.format(0d));
jTextField_TR1.setText(df.format(0d));
}
private void calcular() {
ta1 = Double.parseDouble(jTextField_TA1.getText());
f = Double.parseDouble(jTextField_Fiabilidad.getText()) / 100d;
// Inecuación de Gott
tr0 = ta1 * (Math.abs((f - 1) / (f + 1)));
tr1 = ta1 * (Math.abs((f + 1) / (f - 1)));
// Mostrar
jTextField_TR0.setText(df.format(tr0));
jTextField_TR1.setText(df.format(tr1));
}
public static void main(String args[]) {
java.awt.EventQueue.invokeLater(() -> {
new Main().setVisible(true);
});
}
}
Resultado:
Se muestra diagrama conceptual para entrenamiento de una red neuronal multicapa.
El proceso por pasos:
01- Obtener un Dataset en bruto(raw).
02- Discretizar Dataset [Dataset -> Dataset'].
03- Extraer Entradas(E) y Salidas(D) del Dataset'.
04- Pasar Entradas(E) por la Red Neuronal(RN).
05- Obtener Salidas(Y) de la RN.
06- Calcular Error(δ) en base a las Salidas(Y) de la RN y Salida(D) del Dataset'.
07- En base al cálculo del Error(δ), ajustar pesos(W) de la RN.
08- Pasar al siguiente registro del Dataset' volviendo de nuevo al punto 03. Si no existen más registros se pasa al punto 09.
09- Finalizados los registros del Dataset' volver a posicionarse en el 1º registro y volver a empezar desde punto 03, siempre y cuando el Error(δ) general sea inferior o igual (<=) alumbral especificado por el usuario. En tal caso da por finalizado el entrenaminento.
Tras los posts anteriores (visualizaciones esquemáticas de formulas) el siguiente paso pasa por realizar el cálculo real de todas las variables (salidas, errores y pesos actualizados) partiendo de un dataset(D) de un sólo registro.
Código Java:
package perceptron_p;
import java.util.ArrayList;
import java.util.List;
public class Perceptron_p {
public static void main(String[] args) {
//sketch: num neuronas
List<Integer> nN = new ArrayList<>();
nN.add(2);
nN.add(3);
nN.add(2);
nN.add(1);
double µ = 0.001;
int r = 0; // num. registro del dataset
int nK = nN.size(); // num. de capas = 4
int nE = nN.get(0); // num. de entradas = 2
int nS = nN.get(nK - 1); // num. de salidas = 1
int max = nN.stream().mapToInt(i -> i).max().getAsInt(); // num. max. neuronas por capa
String tmp;
double d_tmp;
// Inicializar dataset (sólo 1 registro o fila)
double[][] D = new double[1][3];
D[0][0] = 0.48d; // entrada 1
D[0][1] = 0.33d; // entrada 2
D[0][2] = 0.81d; // salida 1
// Inicializar pesos W, WBias, Y
double[][][] W = new double[nK][max][max];
double[][] WB = new double[nK][max];
double[][] Y = new double[nK][max];
double[][] E = new double[nK][max];
System.out.println("Inicializar pesos con valores aleatorios:\n");
for (int k = 1; k < nK; k++) {
for (int j = 0; j < nN.get(k); j++) {
for (int i = 0; i < nN.get(k - 1); i++) {
W[k][j][i] = Math.random();
System.out.format("W[%d][%d][%d] = %f\n", k, j, i, W[k][j][i]);
}
WB[k][j] = Math.random();
System.out.format("WB[%d][%d] = %f\n\n", k, j, WB[k][j]);
Y[k][j] = 0.f;
E[k][j] = 0.f;
}
}
// 0.0:-------------------------------------------------------------------
System.out.println("Forward:\n");
int k = 1;
for (int j = 0; j < nN.get(k); j++) {
tmp = "";
d_tmp = 0f;
for (int i = 0; i < nE; i++) {
tmp += String.format("( D[%d][%d] * W[%d][%d][%d] ) + ", r, i, k, j, i);
d_tmp += D[r][i] * W[k][j][i];
}
Y[k][j] = F(d_tmp + (-1 * WB[k][j]), 0);
System.out.format("Y[%d][%d] = F{ %s( -1 * WB[%d][%d] ) } = ", k, j, tmp, k, j);
System.out.println(Y[k][j]);
}
// 0.1:-------------------------------------------------------------------
System.out.println("");
for (k = 2; k < nK; k++) {
for (int j = 0; j < nN.get(k); j++) {
tmp = "";
d_tmp = 0f;
for (int i = 0; i < nN.get(k - 1); i++) {
tmp += String.format("( Y[%d][%d] * W[%d][%d][%d] ) + ", k - 1, i, k, j, i);
d_tmp += Y[k - 1][i] * W[k][j][i];
}
System.out.format("Y[%d][%d] = F{ %s( -1 * WB[%d][%d] ) } = ", k, j, tmp, k, j);
Y[k][j] = F(d_tmp + (-1 * WB[k][j]), 0);
System.out.println(Y[k][j]);
}
System.out.println("");
}
// 1.0:-------------------------------------------------------------------
System.out.println("Backward:\n");
k = nK - 1;
for (int j = 0; j < nS; j++) {
E[k][j] = D[r][nE + j] - Y[k][j];
System.out.format("E[%d][%d] = ( D[%d][%d] - Y[%d][%d] ) = ", k, j, r, nE + j, k, j);
System.out.println(E[k][j]);
}
// 1.1:-------------------------------------------------------------------
System.out.println("");
for (k = k - 1; k > 0; k--) {
for (int j = nN.get(k); j > 0; j--) {
tmp = "";
d_tmp = 0.d;
for (int i = nN.get(k + 1); i > 0; i--) {
tmp += String.format("( E[%d][%d] * W[%d][%d][%d] ) + ", k + 1, i - 1, k + 1, i - 1, j - 1);
d_tmp += E[k + 1][i - 1] * W[k + 1][i - 1][j - 1];
}
System.out.format("E[%d][%d] = %s%s = ", k, j - 1, tmp, "0 ");
System.out.println(d_tmp);
E[k][j - 1] = d_tmp;
}
System.out.println("");
}
// 2.0:-------------------------------------------------------------------
System.out.println("Ajuste pesos:\n");
k = 1;
for (int j = 0; j < nN.get(k); j++) {
for (int i = 0; i < nE; i++) {
W[k][j][i] += (µ * E[k][j] * F(Y[k][j], 1) * D[r][i]);
System.out.format("W'[%d][%d][%d] = W[%d][%d][%d] + ( µ * E[%d][%d] * F'(Y[%d][%d]) * D[%d][%d] ) = ", k, j, i, k, j, i, k, j, k, j, r, i);
System.out.println(W[k][j][i]);
}
WB[k][j] += (µ * E[k][j] * F(Y[k][j], 1) * -1);
System.out.format("WB'[%d][%d] = WB[%d][%d] + ( µ * E[%d][%d] * F'(Y[%d][%d]) * (%d) ) = ", k, j, k, j, k, j, k, j, - 1);
System.out.println(WB[k][j] + "\n");
}
// 2.1:-------------------------------------------------------------------
System.out.println("");
for (k = 2; k < nK; k++) {
for (int j = 0; j < nN.get(k); j++) {
for (int i = 0; i < nN.get(k - 1); i++) {
W[k][j][i] += (µ * E[k][j] * F(Y[k][j], 1) * Y[k - 1][i]);
System.out.format("W'[%d][%d][%d] = W[%d][%d][%d] + ( µ * E[%d][%d] * F'( Y[%d][%d] ) * Y[%d][%d] ) = ", k, j, i, k, j, i, k, j, k, j, k - 1, i);
System.out.println(W[k][j][i]);
}
WB[k][j] += (µ * E[k][j] * F(Y[k][j], 2) * (-1));
System.out.format("WB'[%d][%d] = WB[%d][%d] + ( µ * E[%d][%d] * F'(Y[%d][%d]) * (%d) ) = ", k, j, k, j, k, j, k, j, -1);
System.out.println(WB[k][j] + "\n");
}
System.out.println("");
}
}
// Función Activación - Derivada
private static double F(double n, int op) {
double fx;
switch (op) {
case 0: // función sigmoide
fx = 1.0 / (1.0 + Math.pow(Math.E, -n));
break;
case 1: // derivada función sigmoide
fx = 1.0 / (1.0 + Math.pow(Math.E, -n));
fx = fx * (1 - fx);
break;
default:
fx = 0.f;
break;
}
return fx;
}
}
Resultado:
run:
Inicializar pesos con valores aleatorios:
W[1][0][0] = 0,835049
W[1][0][1] = 0,308429
WB[1][0] = 0,052288
W[1][1][0] = 0,217787
W[1][1][1] = 0,348034
WB[1][1] = 0,588298
W[1][2][0] = 0,961801
W[1][2][1] = 0,796138
WB[1][2] = 0,044188
W[2][0][0] = 0,994101
W[2][0][1] = 0,211034
W[2][0][2] = 0,711812
WB[2][0] = 0,952732
W[2][1][0] = 0,423756
W[2][1][1] = 0,953356
W[2][1][2] = 0,249125
WB[2][1] = 0,973105
W[3][0][0] = 0,842807
W[3][0][1] = 0,794736
WB[3][0] = 0,290240
Forward:
Y[1][0] = F{ ( D[0][0] * W[1][0][0] ) + ( D[0][1] * W[1][0][1] ) + ( -1 * WB[1][0] ) } = 0.6107146316470909
Y[1][1] = F{ ( D[0][0] * W[1][1][0] ) + ( D[0][1] * W[1][1][1] ) + ( -1 * WB[1][1] ) } = 0.40880474360914854
Y[1][2] = F{ ( D[0][0] * W[1][2][0] ) + ( D[0][1] * W[1][2][1] ) + ( -1 * WB[1][2] ) } = 0.6637837549590786
Y[2][0] = F{ ( Y[1][0] * W[2][0][0] ) + ( Y[1][1] * W[2][0][1] ) + ( Y[1][2] * W[2][0][2] ) + ( -1 * WB[2][0] ) } = 0.5530844896875817
Y[2][1] = F{ ( Y[1][0] * W[2][1][0] ) + ( Y[1][1] * W[2][1][1] ) + ( Y[1][2] * W[2][1][2] ) + ( -1 * WB[2][1] ) } = 0.46028147962310223
Y[3][0] = F{ ( Y[2][0] * W[3][0][0] ) + ( Y[2][1] * W[3][0][1] ) + ( -1 * WB[3][0] ) } = 0.6322090580829307
Backward:
E[3][0] = ( D[0][2] - Y[3][0] ) = 0.17779094191706935
E[2][1] = ( E[3][0] * W[3][0][1] ) + 0 = 0.14129683962211012
E[2][0] = ( E[3][0] * W[3][0][0] ) + 0 = 0.1498433870202291
E[1][2] = ( E[2][1] * W[2][1][2] ) + ( E[2][0] * W[2][0][2] ) + 0 = 0.1418609770496571
E[1][1] = ( E[2][1] * W[2][1][1] ) + ( E[2][0] * W[2][0][1] ) + 0 = 0.16632825764793913
E[1][0] = ( E[2][1] * W[2][1][0] ) + ( E[2][0] * W[2][0][0] ) + 0 = 0.2088347664166445
Ajuste pesos:
W'[1][0][0] = W[1][0][0] + ( µ * E[1][0] * F'(Y[1][0]) * D[0][0] ) = 0.8350717767495889
W'[1][0][1] = W[1][0][1] + ( µ * E[1][0] * F'(Y[1][0]) * D[0][1] ) = 0.3084447906938308
WB'[1][0] = WB[1][0] + ( µ * E[1][0] * F'(Y[1][0]) * (-1) ) = 0.05224031629899943
W'[1][1][0] = W[1][1][0] + ( µ * E[1][1] * F'(Y[1][1]) * D[0][0] ) = 0.21780595558207116
W'[1][1][1] = W[1][1][1] + ( µ * E[1][1] * F'(Y[1][1]) * D[0][1] ) = 0.34804701774866154
WB'[1][1] = WB[1][1] + ( µ * E[1][1] * F'(Y[1][1]) * (-1) ) = 0.5882576504954621
W'[1][2][0] = W[1][2][0] + ( µ * E[1][2] * F'(Y[1][2]) * D[0][0] ) = 0.9618160101133663
W'[1][2][1] = W[1][2][1] + ( µ * E[1][2] * F'(Y[1][2]) * D[0][1] ) = 0.7961484238865005
WB'[1][2] = WB[1][2] + ( µ * E[1][2] * F'(Y[1][2]) * (-1) ) = 0.04415614986229021
W'[2][0][0] = W[2][0][0] + ( µ * E[2][0] * F'( Y[2][0] ) * Y[1][0] ) = 0.9941217290526374
W'[2][0][1] = W[2][0][1] + ( µ * E[2][0] * F'( Y[2][0] ) * Y[1][1] ) = 0.21104869817169436
W'[2][0][2] = W[2][0][2] + ( µ * E[2][0] * F'( Y[2][0] ) * Y[1][2] ) = 0.7118355488714299
WB'[2][0] = WB[2][0] + ( µ * E[2][0] * F'(Y[2][0]) * (-1) ) = 0.9527319900854492
W'[2][1][0] = W[2][1][0] + ( µ * E[2][1] * F'( Y[2][1] ) * Y[1][0] ) = 0.4237764313332067
W'[2][1][1] = W[2][1][1] + ( µ * E[2][1] * F'( Y[2][1] ) * Y[1][1] ) = 0.953369304782218
W'[2][1][2] = W[2][1][2] + ( µ * E[2][1] * F'( Y[2][1] ) * Y[1][2] ) = 0.2491472992670435
WB'[2][1] = WB[2][1] + ( µ * E[2][1] * F'(Y[2][1]) * (-1) ) = 0.9731049511389623
W'[3][0][0] = W[3][0][0] + ( µ * E[3][0] * F'( Y[3][0] ) * Y[2][0] ) = 0.8428289253648974
W'[3][0][1] = W[3][0][1] + ( µ * E[3][0] * F'( Y[3][0] ) * Y[2][1] ) = 0.7947544171128877
WB'[3][0] = WB[3][0] + ( µ * E[3][0] * F'(Y[3][0]) * (-1) ) = 0.29024004297076156
BUILD SUCCESSFUL (total time: 2 seconds)
Siguiendo el hilo anterior en esta ocasión se procede ajustar los pesos (W) para minimizar el error. Para ello son utilizadas las siguientes variables:
μ = Tasa de aprendizaje
δ = Error neurona (E)
Ø = Bias (-1)
ʄ = Función de activación
ʄ' = Derivada de la función de activación
ΔW = Delta de los pesos
Función Sigmoide:
ʄ(x) = 1 / ( 1 + e^(-x) )
Derivada función Sigmoide:
ʄ'(x) = ʄ(x) * ( 1 - ʄ(x) )
Cálculo deltas(Δ) de los pesos:
ΔW = µ * δ * ʄ'(x) * Y
ΔW = µ * δ * ʄ'(x) * Ø -> para ajuste pesos del Bias(Ø)
Ajuste pesos:
W' = W + ΔW
Código Java:
package ajustePesos;
import java.util.ArrayList;
import java.util.List;
public class AjustePesos {
public static void main(String[] args) {
//sketch: num neuronas
List<Integer> nN = new ArrayList<>();
nN.add(2);
nN.add(3);
nN.add(2);
nN.add(1);
double µ = 0.001;
int r = 0; // num. registro del dataset
int nK = nN.size(); // num. de capas = 4
int nE = nN.get(0); // num. de entradas = 2
int nS = nN.get(nK - 1); // num. de salidas = 1
String tmp;
// 2.0:-------------------------------------------------------------------
System.out.println("Ajuste pesos:\n");
k = 1;
for (int j = 0; j < nN.get(k); j++) {
for (int i = 0; i < nE; i++) {
System.out.format("W'[%d][%d][%d] = W[%d][%d][%d] + ( µ * E[%d][%d] * F'(Y[%d][%d]) * D[%d][%d] )\n", k, j, i, k, j, i, k, j, k, j, r, i);
}
System.out.format("WB'[%d][%d] = WB[%d][%d] + ( µ * E[%d][%d] * F'(Y[%d][%d]) * %d)\n\n", k, j, k, j, k, j, k, j, - 1);
}
// 2.1:-------------------------------------------------------------------
System.out.println("");
for (k = 2; k < nK; k++) {
for (int j = 0; j < nN.get(k); j++) {
for (int i = 0; i < nN.get(k - 1); i++) {
System.out.format("W'[%d][%d][%d] = W[%d][%d][%d] + ( µ * E[%d][%d] * F'( Y[%d][%d] ) * Y[%d][%d] )\n", k, j, i, k, j, i, k, j, k, j, k - 1, i);
}
System.out.format("WB'[%d][%d] = WB[%d][%d] + ( µ * E[%d][%d] * F'(Y[%d][%d]) * (%d) )\n\n", k, j, k, j, k, j, k, j, -1);
}
System.out.println("");
}
}
}
Resultado:
run:
Ajuste pesos:
W'[1][0][0] = W[1][0][0] + ( µ * E[1][0] * F'(Y[1][0]) * D[0][0] )
W'[1][0][1] = W[1][0][1] + ( µ * E[1][0] * F'(Y[1][0]) * D[0][1] )
WB'[1][0] = WB[1][0] + ( µ * E[1][0] * F'(Y[1][0]) * -1)
W'[1][1][0] = W[1][1][0] + ( µ * E[1][1] * F'(Y[1][1]) * D[0][0] )
W'[1][1][1] = W[1][1][1] + ( µ * E[1][1] * F'(Y[1][1]) * D[0][1] )
WB'[1][1] = WB[1][1] + ( µ * E[1][1] * F'(Y[1][1]) * -1)
W'[1][2][0] = W[1][2][0] + ( µ * E[1][2] * F'(Y[1][2]) * D[0][0] )
W'[1][2][1] = W[1][2][1] + ( µ * E[1][2] * F'(Y[1][2]) * D[0][1] )
WB'[1][2] = WB[1][2] + ( µ * E[1][2] * F'(Y[1][2]) * -1)
W'[2][0][0] = W[2][0][0] + ( µ * E[2][0] * F'( Y[2][0] ) * Y[1][0] )
W'[2][0][1] = W[2][0][1] + ( µ * E[2][0] * F'( Y[2][0] ) * Y[1][1] )
W'[2][0][2] = W[2][0][2] + ( µ * E[2][0] * F'( Y[2][0] ) * Y[1][2] )
WB'[2][0] = WB[2][0] + ( µ * E[2][0] * F'(Y[2][0]) * (-1) )
W'[2][1][0] = W[2][1][0] + ( µ * E[2][1] * F'( Y[2][1] ) * Y[1][0] )
W'[2][1][1] = W[2][1][1] + ( µ * E[2][1] * F'( Y[2][1] ) * Y[1][1] )
W'[2][1][2] = W[2][1][2] + ( µ * E[2][1] * F'( Y[2][1] ) * Y[1][2] )
WB'[2][1] = WB[2][1] + ( µ * E[2][1] * F'(Y[2][1]) * (-1) )
W'[3][0][0] = W[3][0][0] + ( µ * E[3][0] * F'( Y[3][0] ) * Y[2][0] )
W'[3][0][1] = W[3][0][1] + ( µ * E[3][0] * F'( Y[3][0] ) * Y[2][1] )
WB'[3][0] = WB[3][0] + ( µ * E[3][0] * F'(Y[3][0]) * (-1) )
BUILD SUCCESSFUL (total time: 5 seconds)
Descripción:
En base al valor de salida del dataset (D02), se visualiza la base conceptual para el cálculo de los errores (Exx) de cada neurona (Yxx) de una red neuronal tipo perceptrón multicapa. Todo ese proceso se le llama propagación hacia atrás.
Nomenclatura:
Y[k][j]: Salida neurona (capa, posición j-enésima)
E[k][j]: Error neurona (δ) (capa, posición j-enésima)
W[k][j][i]: Peso (capa, neurona destino, neurona origen)
Código Java:
package backward;
import java.util.ArrayList;
import java.util.List;
public class Backward{
public static void main(String[] args) {
//sketch: num neuronas
List<Integer> nN = new ArrayList<>();
nN.add(2);
nN.add(3);
nN.add(2);
nN.add(1);
int r = 0; // num. registro del dataset
int nK = nN.size(); // num. de capas = 4
int nE = nN.get(0); // num. de entradas = 2
int nS = nN.get(nK - 1); // num. de salidas = 1
String tmp;
// 1.0:-------------------------------------------------------------------
System.out.println("Backward:\n");
int k = nK - 1;
for (int j = 0; j < nS; j++) {
System.out.format("E[%d][%d] = ( D[%d][%d] - Y[%d][%d] )\n", k, j, r, nE + j, k, j);
}
// 1.1:-------------------------------------------------------------------
System.out.println("");
for (k = k - 1; k > 0; k--) {
for (int j = nN.get(k); j > 0; j--) {
tmp = "";
for (int i = nN.get(k + 1); i > 0; i--) {
tmp += String.format("( E[%d][%d] * W[%d][%d][%d] ) + ", k + 1, i - 1, k + 1, i - 1, j - 1);
}
System.out.format("E[%d][%d] = %s%s\n", k, j - 1, tmp, "0 ");
}
System.out.println("");
}
}
}
Resultado:
run:
Backward:
E[3][0] = ( D[0][2] - Y[3][0] )
E[2][1] = ( E[3][0] * W[3][0][1] ) + 0
E[2][0] = ( E[3][0] * W[3][0][0] ) + 0
E[1][2] = ( E[2][1] * W[2][1][2] ) + ( E[2][0] * W[2][0][2] ) + 0
E[1][1] = ( E[2][1] * W[2][1][1] ) + ( E[2][0] * W[2][0][1] ) + 0
E[1][0] = ( E[2][1] * W[2][1][0] ) + ( E[2][0] * W[2][0][0] ) + 0
BUILD SUCCESSFUL (total time: 1 second)
Descripción:
En base a los valores de entrada Dxx (dataset), Wxxx (pesos) y WBxx (bias pesos), se visualiza la base conceptual para el cálculo de las salidas de las neuronas (Yxx) de una red neuronal tipo perceptrón multicapa. Todo ese proceso se le llama propagación hacia delante.
Nomenclatura:
Y[k][j]: Salida neurona (capa, posición j-enésima)
W[k][j][i]: Peso (capa, neurona destino, neurona origen)
WB[k][j]: Pesos Bias (capa, posición j-enésima)
F: Función Activación
Dataset:
D[row][col]: Dataset (fila, columna)
0 1 2 col(n)
0 D00 D01 D02 .
1 D10 D11 D12 .
2 D20 D21 D22 .
. . . . .
row(n)
Código Java:
package forward;
import java.util.ArrayList;
import java.util.List;
public class Forward {
public static void main(String[] args) {
//sketch: num neuronas
List<Integer> nN = new ArrayList<>();
nN.add(2);
nN.add(3);
nN.add(2);
nN.add(1);
int r = 0; // num. registro del dataset
int nK = nN.size(); // num. de capas = 4
int nE = nN.get(0); // num. de entradas = 2
int nS = nN.get(nK - 1); // num. de salidas = 1
String tmp;
// 0.0:-------------------------------------------------------------------
System.out.println("Forward:\n");
int k = 1;
for (int j = 0; j < nN.get(k); j++) {
tmp = "";
for (int i = 0; i < nE; i++) {
tmp += String.format("( D[%d][%d] * W[%d][%d][%d] ) + ", r, i, k, j, i);
}
System.out.format("Y[%d][%d] = F{ %s( -1 * WB[%d][%d] ) }\n", k, j, tmp, k, j);
}
// 0.1:-------------------------------------------------------------------
System.out.println("");
for (k = 2; k < nK; k++) {
for (int j = 0; j < nN.get(k); j++) {
tmp = "";
for (int i = 0; i < nN.get(k - 1); i++) {
tmp += String.format("( Y[%d][%d] * W[%d][%d][%d] ) + ", k - 1, i, k, j, i);
}
System.out.format("Y[%d][%d] = F{ %s( -1 * WB[%d][%d] ) }\n", k, j, tmp, k, j);
}
System.out.println("");
}
}
}
Resultado:
run:
Forward:
Y[1][0] = F{ ( D[0][0] * W[1][0][0] ) + ( D[0][1] * W[1][0][1] ) + ( -1 * WB[1][0] ) }
Y[1][1] = F{ ( D[0][0] * W[1][1][0] ) + ( D[0][1] * W[1][1][1] ) + ( -1 * WB[1][1] ) }
Y[1][2] = F{ ( D[0][0] * W[1][2][0] ) + ( D[0][1] * W[1][2][1] ) + ( -1 * WB[1][2] ) }
Y[2][0] = F{ ( Y[1][0] * W[2][0][0] ) + ( Y[1][1] * W[2][0][1] ) + ( Y[1][2] * W[2][0][2] ) + ( -1 * WB[2][0] ) }
Y[2][1] = F{ ( Y[1][0] * W[2][1][0] ) + ( Y[1][1] * W[2][1][1] ) + ( Y[1][2] * W[2][1][2] ) + ( -1 * WB[2][1] ) }
Y[3][0] = F{ ( Y[2][0] * W[3][0][0] ) + ( Y[2][1] * W[3][0][1] ) + ( -1 * WB[3][0] ) }
BUILD SUCCESSFUL (total time: 0 seconds)
En Java no existe el concepto de Listas Multidimensionales. Para ello mediante código se puede simular listas multidimensionales creando listas dentro de otras listas:
List<List<Double>> dataset1 = new ArrayList<List<Double>>();
En el ejemplo se crea una tabla de 3x10 mediante listas con la que se llenará con valores numéricos para luego imprimirlo en pantalla.
Código (DataSets1.java):
package datasets1;
import java.util.ArrayList;
import java.util.List;
public class DataSets1 {
public static void main(String[] args) {
//Dataset 2d
List<List<Double>> dataset1 = new ArrayList<List<Double>>();
//Agregar 3 sublistas (columnas)
for (int i = 0; i < 3; i++) {
dataset1.add(new ArrayList<Double>());
}
/*
@ Añadir datos al dataset (suma)
*/
//operando 1
dataset1.get(0).add(48.0);
dataset1.get(0).add(1.0);
dataset1.get(0).add(41.0);
dataset1.get(0).add(6.0);
dataset1.get(0).add(5.0);
dataset1.get(0).add(18.0);
dataset1.get(0).add(35.0);
dataset1.get(0).add(2.0);
dataset1.get(0).add(44.0);
dataset1.get(0).add(24.0);
//operando 2
dataset1.get(1).add(33.0);
dataset1.get(1).add(38.0);
dataset1.get(1).add(25.0);
dataset1.get(1).add(27.0);
dataset1.get(1).add(42.0);
dataset1.get(1).add(12.0);
dataset1.get(1).add(39.0);
dataset1.get(1).add(17.0);
dataset1.get(1).add(14.0);
dataset1.get(1).add(37.0);
//resultado 1
dataset1.get(2).add(81.0);
dataset1.get(2).add(39.0);
dataset1.get(2).add(66.0);
dataset1.get(2).add(33.0);
dataset1.get(2).add(47.0);
dataset1.get(2).add(30.0);
dataset1.get(2).add(74.0);
dataset1.get(2).add(19.0);
dataset1.get(2).add(58.0);
dataset1.get(2).add(61.0);
//imprimir dataset1
System.out.println("'operando1', 'operando2', 'resultado1'");
for (int i = 0; i <= dataset1.get(0).size() - 1; i++) {
for (int j = 0; j < dataset1.size(); j++) {
System.out.print(dataset1.get(j).get(i) + ";\t");
}
System.out.println("");
}
}
}
Resultado:
run:
'operando1', 'operando2', 'resultado1'
48.0; 33.0; 81.0;
1.0; 38.0; 39.0;
41.0; 25.0; 66.0;
6.0; 27.0; 33.0;
5.0; 42.0; 47.0;
18.0; 12.0; 30.0;
35.0; 39.0; 74.0;
2.0; 17.0; 19.0;
44.0; 14.0; 58.0;
24.0; 37.0; 61.0;
BUILD SUCCESSFUL (total time: 0 seconds)
Desde Netbeans en modo diseño se añaden los componentes siguiendo esta estructura:
-----------------------------------------------------------------
. JFrame (title: "Graficando perceptrón")
. jPanel1 (aqui se graficará la red neuronal)
. jToolBar1 (barra de opciones)
. jLabel1 (texto: "Estructura")
. jTextField1 (texto: "2,4,4,1")
. jButton1 (texto: "Graficar")
. jButton2 (texto: "Limpiar")
-----------------------------------------------------------------
Código 1 (Muro.java):
package centrar;
public class Muro extends javax.swing.JFrame {
public Muro() {
initComponents();
this.setLocationRelativeTo(null);
}
private void initComponents() { ... } // <- código generado automáticament por Netbeans
private void jButtonGraficarActionPerformed(java.awt.event.ActionEvent evt) {
Dibujar t = new Dibujar(jPanel1.getGraphics(), jPanel1.getWidth(), jPanel1.getHeight(), jTextField1.getText());
}
private void jButtonLimpiarActionPerformed(java.awt.event.ActionEvent evt) {
this.jPanel1.repaint();
}
public static void main(String args[]) {
java.awt.EventQueue.invokeLater(new Runnable() {
public void run() {
new Muro().setVisible(true);
}
});
}
private javax.swing.JButton jButtonGraficar;
private javax.swing.JButton jButtonLimpiar;
private javax.swing.JLabel jLabel1;
private javax.swing.JPanel jPanel1;
private javax.swing.JToolBar.Separator jSeparator1;
private javax.swing.JToolBar.Separator jSeparator2;
private javax.swing.JTextField jTextField1;
private javax.swing.JToolBar jToolBar1;
}
Código 2 (Dibujar.java):
package centrar;
import java.awt.BasicStroke;
import java.awt.Color;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.RenderingHints;
import java.awt.Stroke;
import java.util.ArrayList;
import java.util.List;
public class Dibujar {
Graphics g;
Graphics2D g2;
public Dibujar(Graphics g, int width, int height, String estruct) {
g2 = (Graphics2D) g;
g2.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);
g2.setColor(Color.BLACK);
// tipos grosores pinceles
Stroke stroke02 = new BasicStroke(0.2f);
Stroke stroke04 = new BasicStroke(0.4f);
g2.setStroke(stroke02);
// añadir datos estructura perceptrón
List<Integer> estructura = new ArrayList<>();
for (String aux1 : estruct.split(",")) {
estructura.add(Integer.parseInt(aux1));
}
int maxX = estructura.size();
int maxY = maximo(estructura);
int nParticionesX = maxX + 2; // se suma 2 para margen superior e inferior
int nParticionesY = maxY + 2; // se suma 2 para margen superior e inferior
int uX = width / nParticionesX;
int uY = height / nParticionesY;
float uSeparadorX = (nParticionesX - estructura.size()) / 2f;
float uSeparadorY;
int posIniX = (int) Math.round(uX * uSeparadorX);
int posIniY;
int[][][] recopilador = new int[maxX][maxY][2]; // k, x, y
// capa 0: pre-logical posiciones
for (int x = 0; x < estructura.size(); x++) {
for (int y = 0; y < estructura.get(x); y++) {
uSeparadorY = (nParticionesY - estructura.get(x)) / 2f;
posIniY = (int) Math.round(uY * uSeparadorY);
recopilador[x][y][0] = (posIniX + (int) uX * x) + (int) (uX / 2);
recopilador[x][y][1] = (posIniY + (int) uY * y) + (int) (uY / 2);
}
}
// capa 1: graficar neuronas
int radio = (int) Math.round(uY / 2f);
for (int x = 0; x < estructura.size(); x++) {
for (int y = 0; y < estructura.get(x); y++) {
centrarCirculo(g2, recopilador[x][y][0], recopilador[x][y][1], radio);
}
}
// capa 2: graficar enlaces
int x1, y1, x2, y2;
g2.setColor(Color.DARK_GRAY);
g2.setStroke(stroke04);
for (int x = 0; x < estructura.size() - 1; x++) {
for (int y = 0; y < estructura.get(x); y++) {
for (int k = 0; k < estructura.get(x + 1); k++) {
x1 = recopilador[x][y][0];
y1 = recopilador[x][y][1];
x2 = recopilador[x + 1][k][0];
y2 = recopilador[x + 1][k][1];
g2.drawLine(x1, y1, x2, y2);
}
}
}
}
private void centrarCirculo(Graphics g2, int x, int y, int r) {
x = x - (r / 2);
y = y - (r / 2);
g2.fillOval(x, y, r, r);
}
/* Busca número mayor del listado de la estructura
* Utilizado para acomodar la gráfica al tamaño de la ventana
*/
private int maximo(List<Integer> estructura) {
int max = 0;
for (int i = 0; i < estructura.size(); i++) {
if (estructura.get(i) >= max) {
max = estructura.get(i);
}
}
return max;
}
}
Resultado:

Desde Netbeans y en modo diseño se agrega un jFrame con la opción marcada "Grid Layout" y en propiedades activamos el check [v] undecorated. Se añade luego un jPanel que servirá de lienzo para graficar el tablero.
Para las figuras he instalado una fuente gratuita llamada "Chess Cases".
Código1 (Tabla.java):
package ajedrez;
public class Tabla extends javax.swing.JFrame {
public Tabla() {
initComponents();
this.setBounds(0, 0, 512, 512);
this.setLocationRelativeTo(null);
this.jPanel1.setBounds(0, 0, 512, 512);
this.jPanel1.setBackground(new java.awt.Color(190, 190, 190));
}
private void initComponents() { ... } // Código generado automáticamente por Netbeans.
private void jPanel1MouseClicked(java.awt.event.MouseEvent evt) {
Dibujar t = new Dibujar(jPanel1.getGraphics(), this.jPanel1.getWidth());
}
public static void main(String args[]) {
java.awt.EventQueue.invokeLater(new Runnable() {
public void run() {
new Tabla().setVisible(true);
}
});
}
private javax.swing.JPanel jPanel1;
}
Código2 (Dibujar.java):
package ajedrez;
import java.awt.BasicStroke;
import java.awt.Color;
import java.awt.Font;
import java.awt.FontMetrics;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.Rectangle;
import java.awt.RenderingHints;
import java.awt.Stroke;
public class Dibujar {
Rectangle rect = new Rectangle();
public Dibujar(Graphics g, int xy) {
Graphics2D g2 = (Graphics2D) g;
g2.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);
g2.setColor(Color.GRAY);
// Crea tablero
int casillas = 8;
int radio = xy / casillas;
for (int j = 0; j < casillas; j++) {
for (int i = 0; i < casillas; i++) {
if ((j % 2) != 0) {
g2.fillRect(2 * radio * i, radio * j, radio, radio);
}
if ((i % 2 != 0)) {
g2.fillRect(radio * i, 2 * radio * j, radio, radio);
}
}
}
// Remarcar contorno
Stroke pincel = new BasicStroke(2f);
g2.setColor(Color.BLACK);
g2.setStroke(pincel);
g2.drawRect(0, 0, xy - 1, xy - 1);
// Piezas
Font font = new Font("Chess Cases", Font.TRUETYPE_FONT, 46);
String piezas = "tmvwlvmt";
for (int i = 0; i < casillas; i++) {
// Inserción piezas negras
g.setColor(Color.BLACK);
rect.setBounds(radio * i, 0, radio, radio);
centrarTexto(g, piezas.charAt(i) + "", rect, font);
rect.setBounds(radio * i, radio, radio, radio);
centrarTexto(g, "o", rect, font);
// Inserción piezas blancas
g.setColor(Color.WHITE);
rect.setBounds(radio * i, radio * 7, radio, radio);
centrarTexto(g, piezas.charAt(i) + "", rect, font);
rect.setBounds(radio * i, radio * 6, radio, radio);
centrarTexto(g, "o", rect, font);
}
}
private void centrarTexto(Graphics g, String texto, Rectangle r, Font f) {
FontMetrics medir = g.getFontMetrics(f);
int x = r.x + (r.width - medir.stringWidth(texto)) / 2;
int y = r.y + ((r.height - medir.getHeight()) / 2) + medir.getAscent();
g.setFont(f);
g.drawString(texto, x, y);
}
}
Resultado:
Desde Netbeans y en modo diseño se agrega un jFrame con la opción marcada "Grid Layout" y en propiedades activamos el check [v] undecorated. Se añade luego un jPanel, que servirá de lienzo para graficar. Algoritmo claramente mejorable de ahí que lo he puesto versión beta.
Código1 (Muro.java):
package pasapalabra;
public class Muro extends javax.swing.JFrame {
public Muro() {
initComponents();
this.setBounds(0, 0, 512, 512);
this.jPanel1.setBounds(0, 0, 512, 512);
this.setLocationRelativeTo(null);
this.repaint();
}
private void initComponents() { ... }// Código generado automáticamente por Netbeans
private void jPanel1MouseClicked(java.awt.event.MouseEvent evt) {
double grados = 0;
Dibujar t = new Dibujar(jPanel1.getGraphics(), this.jPanel1.getWidth() / 2, this.jPanel1.getHeight() / 2, grados);
Instrucciones(t);
}
public static void main(String args[]) {
java.awt.EventQueue.invokeLater(() -> {
new Muro().setVisible(true);
});
}
private javax.swing.JPanel jPanel1;
// Instrucciones tipo tortuga que dibuja
private void Instrucciones(Dibujar t) {
int n = 25;
String letras = "GFEDCBAZYXVUTSRQPOÑNMLJIH";
double x0, y0, r, grado;
r = jPanel1.getWidth() / 2.5f;
x0 = jPanel1.getWidth() / 2;
y0 = jPanel1.getHeight() / 2;
// Ángulo en radianes (importante)
grado = (2 * Math.PI) / n;
// Dibuja rosco pasapalabra
t.gira(0);
for (int i = 0; i < n; i++) {
t.avanza(r);
t.figura(letras.charAt(i));
t.salta(x0, y0);
t.gira(grado);
}
}
}
Código2 (Dibujar.java):
package pasapalabra;
import java.awt.Color;
import java.awt.Font;
import java.awt.FontMetrics;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.Rectangle;
import java.awt.RenderingHints;
public class Dibujar {
double x, y, angulo;
Graphics g;
Graphics2D g2;
Rectangle rect = new Rectangle();
public Dibujar(Graphics g, double x, double y, double angulo) {
this.x = x;
this.y = y;
this.angulo = angulo;
this.g = g;
g2 = (Graphics2D) g;
// Filtro "antialiasing"
g2.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);
}
public void gira(double angulo) {
this.angulo += angulo;
}
public void figura(char letra) {
int r = 45; // Radio
double x2 = x - (r / 2);
double y2 = y - (r / 2);
g.setColor(Color.BLUE);
g.fillOval((int) x2, (int) y2, r, r);
g.setColor(Color.WHITE);
rect.setBounds((int) x2, (int) y2, r, r);
centrarTexto(g, "" + letra, rect, new Font("", Font.BOLD, 26));
}
public void avanza(double distancia) {
double x2 = x + distancia * Math.cos(angulo);
double y2 = y - distancia * Math.sin(angulo);
salta(x2, y2);
}
public void salta(double x, double y) {
this.x = x;
this.y = y;
}
private void centrarTexto(Graphics g, String texto, Rectangle r, Font f) {
FontMetrics medir = g.getFontMetrics(f);
int x = r.x + (r.width - medir.stringWidth(texto)) / 2;
int y = r.y + ((r.height - medir.getHeight()) / 2) + medir.getAscent();
g.setFont(f);
g.drawString(texto, x, y);
}
}
Resultado:

Desde Netbeans y en modo diseño se agrega un jFrame con la opción marcada "Grid Layout". Se añade luego un jPanel, que servirá de lienzo para graficar. Algoritmo claramente mejorable de ahí que lo he puesto versión beta.
Código1 (Muro.java):
package triangulopascal_2d;
public class Muro extends javax.swing.JFrame {
public Muro() {
this.setUndecorated(true);
initComponents();
this.setBounds(0, 0, 513, 513);
this.jPanel1.setBounds(0, 0, 512, 512);
this.setLocationRelativeTo(null); // Centrar pantalla
this.repaint();
}
private void initComponents() { ... }
private void formMouseClicked(java.awt.event.MouseEvent evt) {
TrianguloPascal.Dibujar(jPanel1.getGraphics(), this.jPanel1.getWidth());
}
public static void main(String args[]) {
java.awt.EventQueue.invokeLater(new Runnable() {
public void run() {
new Muro().setVisible(true);
}
});
}
// Variables declaration - do not modify
private javax.swing.JPanel jPanel1;
// End of variables declaration
}
Código2 (TrianguloPascal.java):
package triangulopascal_2d;
import java.awt.Color;
import java.awt.Graphics;
import java.awt.Graphics2D;
public class TrianguloPascal {
public static void Dibujar(Graphics g, float xy) {
Graphics2D g2 = (Graphics2D) g;
// Inicialización variables
int u = (int) xy / 32;
int a = 1, b = 29, c = 29;
int[] d1 = triangulo();
int indice = 118;
// Dibuja pirámide de bloques
while (a <= b) {
for (int i = a; i <= b; i = i + 2) {
g2.setColor(Color.BLUE);
g.fillRect(i * u + 1, c * u + 1, 2 * u - 1, 2 * u - 1);
g2.setColor(Color.WHITE);
if (indice >= 0) {
g.drawString(String.format("%1$5s", d1[indice]), i * u, c * u + 20);
} else {
g.drawString(String.format("%1$5s", d1[0]), i * u, c * u + 20);
}
indice--;
}
a++;
b--;
c = c - 2;
}
}
private static int[] triangulo() {
int[] d1 = new int[119];
int[][] d2 = new int[16][16];
d2[1][1] = 1;
int indice = 0;
for (int j = 2; j < 16; j++) {
for (int i = 1; i < 16; i++) {
d2[j][i] = d2[j - 1][i - 1] + d2[j - 1][i];
if (d2[j][i] != 0) {
d1[indice] = d2[j][i];
indice++;
}
}
}
d1[0] = 1;
return d1;
}
}
Resultado: